Back to the course home page
Specifying how many things are F
There are at least ___ F's
One: ( x)
Fx
x)
Fx
Two: ( x)
(
x)
( y)
(Fx & Fy & x
y)
(Fx & Fy & x
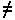 y)
y)
Three: ( x)
(
x)
( y)
(
y)
( z)
(Fx & Fy & Fz & x
z)
(Fx & Fy & Fz & x
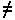 y & x
y & x
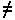 z & y
z & y
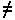 z)
z)
Four: ( x)
(
x)
( y)
(
y)
( z)
(
z)
( w)
(Fx & Fy & Fz & Fw & x
w)
(Fx & Fy & Fz & Fw & x
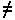 y & x
y & x
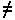 z & x
z & x
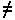 w & y
w & y
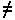 z & y
z & y
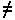 w & z
w & z
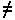 w)
w)
n: ( x1)
...
(
x1)
...
( xn)
(Fx1 & ... & Fxn & x1
xn)
(Fx1 & ... & Fxn & x1
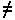 x2 & ... & xn-1
x2 & ... & xn-1
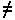 xn)
xn)
There are at most ___ F's
One way to say "at most n things are F" is to say
~ "at least n+1 things are F"
by using the symbolization above. Another way is to say it
directly.
One: (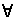 x)
(
x)
(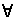 y)
[(Fx & Fy)
y)
[(Fx & Fy) 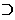 x = y]
x = y]
Two: (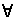 x)
(
x)
(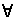 y)
(
y)
(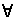 z)
[(Fx & Fy & Fz)
z)
[(Fx & Fy & Fz) 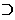 (x = y v x = z v y = z )]
(x = y v x = z v y = z )]
Three: (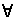 x)
(
x)
(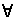 y)
(
y)
(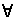 z)
(
z)
(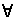 w)
[(Fx & Fy & Fz & Fw)
w)
[(Fx & Fy & Fz & Fw) 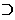 (x = y v x = z v x = w v y = z v y = w v z = w)]
(x = y v x = z v x = w v y = z v y = w v z = w)]
n: (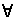 x1)
...
(
x1)
...
(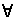 xn+1)
[(Fx1 & ... & Fxn+1)
xn+1)
[(Fx1 & ... & Fxn+1) 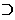 (x1 = x2 v x1 = x3
v ... v x1 = xn+1 v
x2 = x3 v ... v x2 = xn+1
v ... v xn = xn+1)]
(x1 = x2 v x1 = x3
v ... v x1 = xn+1 v
x2 = x3 v ... v x2 = xn+1
v ... v xn = xn+1)]
There are exactly ___ F's
One way is to say "exactly n things are F" is to say
"at least n things are F"
& "at most n things are F"
by using the symbolizations above.
Another way is to say it directly:
Zero: (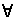 x)
(~Fx)
x)
(~Fx)
One: ( x)
(
x)
(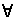 y)
[Fx &
(Fy
y)
[Fx &
(Fy 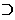 y = x)]
y = x)]
Two: ( x)
(
x)
( y)
(
y)
(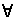 z)
{Fx & Fy &
[Fz
z)
{Fx & Fy &
[Fz 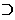 (z = x v z = y)]
& x
(z = x v z = y)]
& x 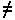 y}
y}
Three: ( x)
(
x)
( y)
(
y)
( z)
(
z)
(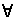 w)
{Fx & Fy & Fz &
[Fw
w)
{Fx & Fy & Fz &
[Fw 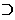 (w = x v w = y v w = z)]
& x
(w = x v w = y v w = z)]
& x 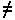 y
& x
y
& x 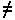 z
& y
z
& y 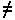 z}
z}
n: ( x1)
...
(
x1)
...
( xn)
(
xn)
(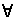 y)
{Fx1 & ... & Fn &
[Fy
y)
{Fx1 & ... & Fn &
[Fy 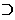 (y = x1 v ... v y = xn)]
& x1
(y = x1 v ... v y = xn)]
& x1
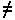 x2 & ... & xn-1
x2 & ... & xn-1
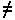 xn}
xn}
Specifying how many things there are
This can be done using the symbolizations above, but leaving out the F's. For instance,
"There are at least 2 things [in the UD]" may be symbolized
( x)
(
x)
( y)
(x
y)
(x
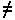 y)
y)